
Gaussian 03 Online Manual
Last update: 2 October 2006
CID
CISD

These method keywords request a Hartree-Fock calculation followed by configuration interaction with all double substitutions (CID) or all single and double substitutions (CISD) from the Hartree-Fock reference determinant [61,143,202]. CIDS and CI are synonyms for CISD.

FC
All frozen core options are available with CID and CISD.
Conver=N
Sets the convergence calculations to 10-N on the energy and 10-(N+2)
on the wavefunction. The default is N=7 for single points and N=8
for gradients.
MaxCyc=n
Specifies the maximum number of
cycles for CISD calculations.

Energies, analytic gradients, and numerical frequencies.


The CI energy appears in the output as follows:
DE(CI)= -.48299990D-01 E(CI)= -.75009023292D+02 NORM(A) = .10129586D+01
The output following the final CI iteration gives the predicted total energy. The second output line displays the value of Norm(A). Norm(A)-1 gives a measure of the correlation correction to the wavefunction; the coefficient of the HF configuration is thus 1/Norm(A). Note that the wavefunction is stored in intermediate normalization; that is:
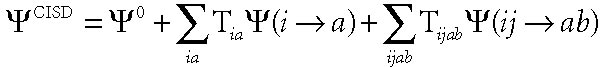
where Ψ0 is the Hartree-Fock determinant and has a coefficient of 1 (which is what intermediate normalization means). Norm(A) is the factor by which to divide the wavefunction as given above to fully normalize it. Thus:
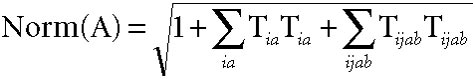
The coefficient of the Hartree-Fock determinant in the fully normalized wavefunction is then 1/Norm(A), the coefficient of singly-excited determinantΨi→a is Tia/Norm(A), and so on.